|
|
6. Bibliography / Appendix::
Bibliography:
[APO]
Apostol, Tom M., Modular Functions and Dirichlet Series in Number
Theory 2nd Ed. Springer-Verlag; London, New York, 1990. Chapters
1-3.
[GGT] Gordon,
D; Grenier, D; Terras, A., “Hecke Operators and the Fundamental Domain for
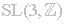.” Mathematics of Computation Vol. 48, 1987, Pages 159-178.
[GRE] Grenier,
D., Fundamental Domains for
, Ph.D. Thesis, Univ. of California at San Diego, June, 1986.
[MAA] Maass,
H., “Siegal’s Modular Forms and Dirichlet Series.” Lecture Notes in Math.,
vol. 216, Springer-Verlag, Berlin and New York, 1971.
Appendix:
A1.
*The
output to the program is a list of powers of T. Applying them left to right on z and S between
each T will result in the final output,
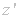contained in the F2*
z
:= 5.875 + 0.00002*I:
Digits
:= 20:
z
:= simplify(evalc(z)):
A
:= array(1..50):
A[1]
:= -round(Re(z)):
z
:= z +A[1]:
m
:= 2:
while
abs(evalf(z)) < 1 do
z := simplify(evalc(-1/z)):
A[m] := -evalc(Re(round(evalc(z)))):
z := z +A[m]:
m := m+1:
od:
for
q from 1 to m do
print(A[q]);
od:
print(z);
*End
of Algorithm*
A2.
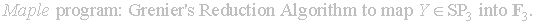
*The
output of this program is a list of each steps matrix Y, the final Y
is contained in the fundamental region
F3*
*We
begin by defining all matrices needed for the algorithm*
restart;
with(linalg):
S
:= matrix((2,2,[0,1,-1,0])):
T
:= matrix((2,2,[1,1,0,1])):
s[1]
:= matrix((3,3,[0,0,1,1,0,0,0,1,0])):
s[2]
:= matrix((3,3,[0,1,0,0,0,1,1,0,0])):
s[3]
:= matrix((3,3,[0,1,0,1,0,-1,-1,0,0])):
s[4]
:= matrix((3,3,[1,0,0,-1,1,0,1,0,1])):
s[5]
:= matrix((3,3,[1,0,0,0,0,1,0,-1,0])):
t[1]
:= matrix((3,3,[1,1,0,0,1,0,0,0,1])):
t[2]
:= matrix((3,3,[1,0,1,0,1,0,0,0,1])):
t[3]
:= matrix((3,3,[1,0,0,0,1,1,0,0,1])):
u[1]
:= matrix((3,3,[1,0,0,0,-1,0,0,0,-1])):
Iden
:= array(identity, 1..3,1..3):
s[0]
:= Iden:
*Next
the equations to find each coordinate during calculations*
y1
:= Y[1,1]:
y2
:= Y[2,2]-(Y[1,2]^2)/Y[1,1]:
y3
:= Y[3,3]-(Y[1,3]^2/Y[1,1])-((Y[1,1]*Y[2,3]-
Y[1,2]*Y[1,3])^2/(Y[1,1]^2*Y[2,2]-[1,1]*Y[1,2]^2)):
x1
:= Y[1,2]/Y[1,1]:
x2
:= Y[1,3]/Y[1,1]:
x3
:= (Y[1,1]*Y[2,3]-Y[1,2]*Y[1,3])/(Y[1,1]*Y[2,2]-Y[1,2]^2):
*Here
we define our matrix Y by y-temp and x-temp the canonical form*
Yt
:= matrix((3,3,[22,0,0,0,1/11,0,0,0,1/2])):
Xt
:= matrix((3,3,[1,-24/5,1/125,0,1,85/3,0,0,1])):
print(Yt,
Xt);
Y
:= multiply(transpose(Xt),Yt,Xt);
*Now
we begin the algorithm*
temp1
:= Iden:
j
:= 0:
print(Initial,
Yis, Y);
while
not equal(Y,temp1) do
j := j+1:
temp1 := evalm(Y):
te[0] := Y:
te[1] := multiply(transpose(s[1]),Y,s[1]):
te[2] := multiply(transpose(s[2]),Y,s[2]):
te[3] := multiply(transpose(s[3]),Y,s[3]):
te[4] := multiply(transpose(s[4]),Y,s[4]):
Stemp := 10^20:
temp := 0:
for i from 0 to 4
do if (te[i][1,1] <= Stemp)
then Stemp := te[i][1,1]:
temp := i:
fi:
od:
print(Step, j,1, Vis, Se,temp):
Y := multiply(transpose(s[temp]),Y,s[temp]):
print(Step, j,1, Yis, Y);
w := (y1^(1/2))*y2:
z := x3 +(1/w)*I:
print(Step, j,2, Zis, z);
Digits := 20:
z := simplify(evalc(x3+(1/w)*I)):
A := array(1..50):
A[1] := -round(Re(z)):
z := z +A[1]:
m := 2:
while abs(evalf(z)) < 1 do
z := simplify(evalc(-1/z)):
A[m] := -evalc(Re(round(evalc(z)))):
z := z +A[m]:
m := m+1:
od:
for q from 1 to m do
print(A[q]);
od:
print (Mis, m);
gamma1 := Iden:
for i from 1 to m-2 do:
if A[i] <> 0 then
gamma1 := multiply(evalm(t[3]^A[i]),gamma1):
fi:
gamma1 := multiply(s[5],gamma1):
od:
if A[m-1] <> 0 then
gamma1 := multiply(evalm(t[3]^A[i]),gamma1):
fi:
print(Step, j,2, gamma1is, gamma1);
Y := multiply(transpose(gamma1),Y,gamma1):
print(Step, j,2, Yis, Y);
p1 := floor(.5-x1):
p2 := floor(.5-x2):
print(step, j,3, p1is, p1, p2is, p2);
gamma2 := Iden:
if p1 <>0 and p2 <> 0 then
gamma2 := multiply(evalm(t[1]^(p1)),evalm(t[2]^(p2))):
elif p1 <> 0 then
gamma2 := evalm(t[1]^(p1)):
elif p2 <> 0 then
gamma2 := evalm(t[2]^(p2)):
fi:
print(Step, j,3, gamma2is, gamma2);
Y := multiply(transpose(gamma2),Y,gamma2):
print(Step, j,3, Yis, Y);
if x1 <0 then
Y := multiply(transpose(u[1]),Y,u[1]):
print(Step, j,4, Yis, Y);
fi:
print(End, Step, j, Yis, Y);
od:
print(Final,
Y1is, y1, Y2is, y2, Y3is, y3, X1is, x1, X2is, x2, X3is, x3);
*End
of Algorithm*