|
|
1. Classical Möbius Transformations:
We
begin our look at
by the classical method of
examining Möbius transformations. It
is due to our familiarity of these transformations and their action on the upper
half-plane that allow us to progress into the cleaner matrix form and
.
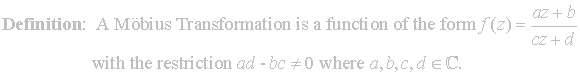
Multiplying all coefficients a,b,c,d by a nonzero constant does not change a Möbius transformation, thus there is no loss of generality in assuming that ad - bc = 1
Next we note how Möbius transformations are related to matrices. Given a
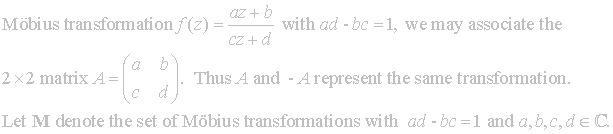
So
composition of functions is associated with matrix multiplication and thus is
associative over M. The
identity matrix
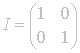is associated with the identity
transformation
. Similarly the matrix inverse
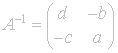is associated to the inverse of f,
. Therefore we have proven the
following theorem.
Theorem
1.1: The set of Möbius Transformations M form a group under
composition.
Now
that we have associated matrices with the group of Möbius transformations, we
will define our matrix group
.
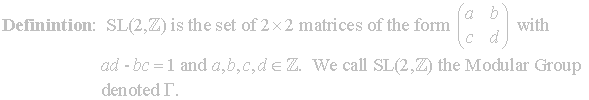
Next
we shall consider
by
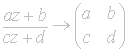. Clearly f is injective and
surjective, and we have seen group operations hold, thus f is an
isomorphic function and
. Thus proving the next theorem.
Consequently
Γ acts on the upper half-plane in the same way as a Möbius transformation.
So we define the action for
.
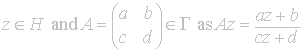We
now abandon the familiar Möbius transformations for the cleaner form of
matrices as we continue to develop notation to present fundamental regions. We will show that Γ is generated by two elements, thus
we will only need to consider their action on the upper half-plane as we present
an algorithm to find a matrix to map any point in the upper half-plane into that
region.
It
will become more obvious later how T and S act upon points of the
upper half-plane, however we will quickly note their action here.
is a
shift of ‘n’ units along the real axis: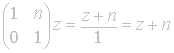 
;
and S is a negative inversion: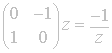 
.
We
also note that the inverse of S is itself and the inverse of
is
. We
now turn our attention toward identifying
with
the upper half-plane. First we will need to recall some familiar definitions.
with
the upper half-plane.
Let K denote the set of orthogonal
matrices
and Z denote the center of
. It
follows that the elements of K are of the form
where
and the
elements of Z are of the form
Also,
one can easily show that K and Z are both subgroups of
. Thus
the group ZK, which is of the form
is a
subgroup of
. We
now let
, which will be identified with the upper half-plane.
We
will refer to this form as the canonical form since we will, in the next
theorem, identify the associated coordinates in the upper half-plane with this
matrix form. We
will often return to this canonical form during calculations.
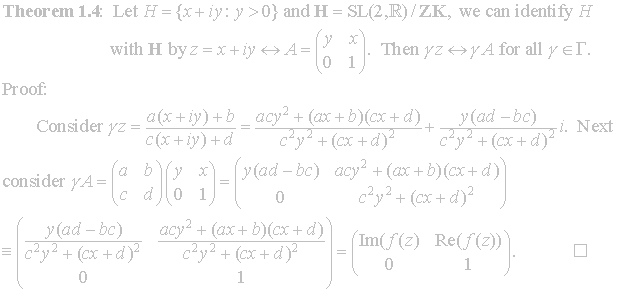
Now
that we have
identified
with the upper half-plane we proceed to a fundamental region and explore how
acts on
the upper half-plane.