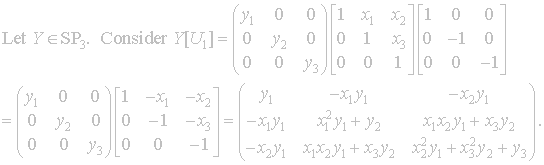|
|
4. A Fundamental Region for
:
We
begin our investigation of
by first exploring another form of
. It is from this form that we find
our approach to a fundamental region for
. For this we first define SPn.
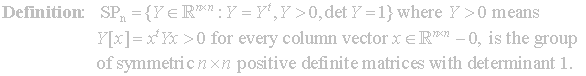
One
may show that the elements of SP2 may be written in the form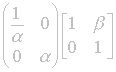 
, which will indeed be our new form. This
new form will be identified with the upper half-plane in the same fashion as we
have identified
, an element of the upper half-plane, with the matrix
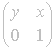. We will use this new form as we
investigate
. This form can be easily
generalized to
.
We
identify
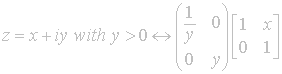where
. Since it is often difficult to
return to the form during calculations, we note that in expanded form
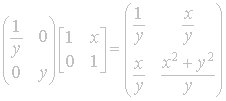, so we can easily identify the real and imaginary parts by
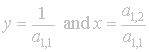where
are the positions of our new
matrix. For
and
we define the action of Γ on
SP2 to be
.
To show that all previous results hold, we will show that S and T act the same on this new form.
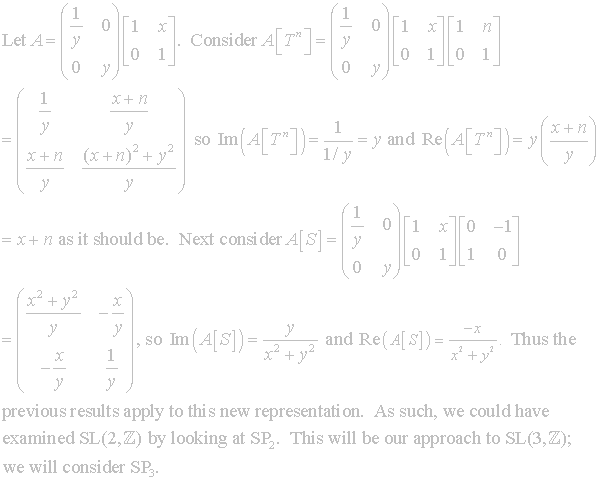
Let
Z and K be as before only in the 3´3
dimension. Then we have the mapping
given by
In the
case we had left action on H;
here we follow the form of Maass [MAA], Siegel, Gordon, Grenier, and
Terras [GGT] with right action of
on SP3.
Elements of SP3 are of the form:
As
before, it is difficult to return to canonical form (4.1), so we will present
equations to find the coordinates, which will be very helpful during
calculations.
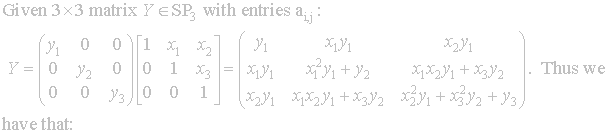
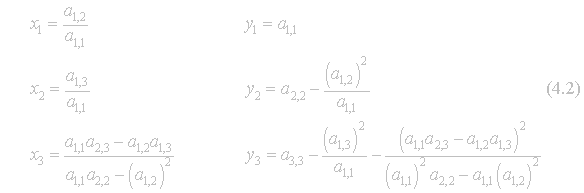
Now
we will consider a fundamental region for
. There
have been a number of such found, however we will only look at Grenier’s
fundamental region [GRE].
Note that since
has
order 2 with the nontrivial coset
–I3.
Since
for Y
an element of SP3, the fundamental region for
is also
a fundamental region for
. Grenier
also has developed a reduction algorithm [GRE] to move elements Y
of SP3 into this fundamental region.
Greiner’s
Fundamental Region for
is as follows:
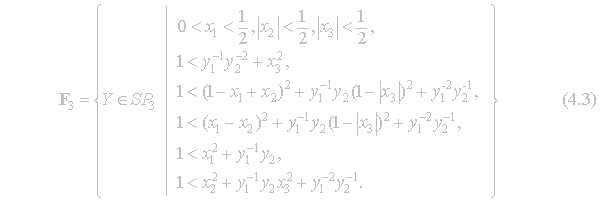
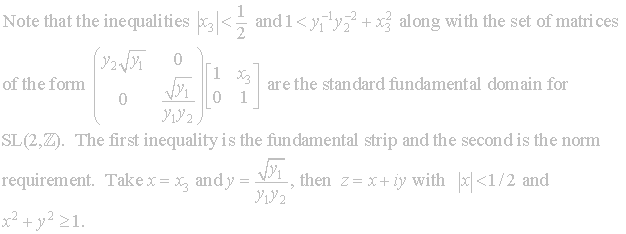
Next
we will explore the generators of
as found in Gordon, Grenier, and Terras [GGT].
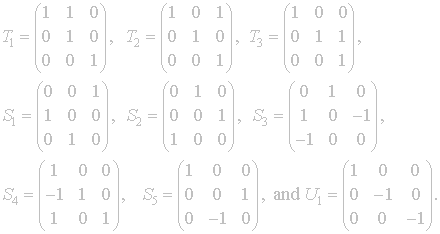
Now
we examine how these matrices act on elements of SP3.
Now we will consider S1.
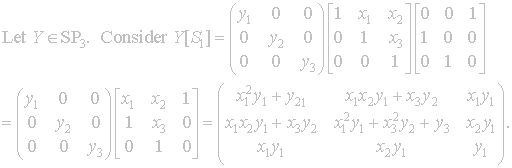
S1
moves the entries of Y and as such dramatically changes the values of the
coordinates. The
rest of the S matrices are considerably harder to see, they move the
entries of Y as well as change the values of the entries.
However we can again notice that
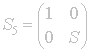for
generator S of Γ.
Finally
we examine U1, it insures
in the algorithm by changing the signs on the x-coordinates.
