|
|
|
2. Fundamental Region:
We
will begin this section by defining the fundamental region for any group G.
In order to do this we will need to define what is meant for two points
to be equivalent under the action of the group G.
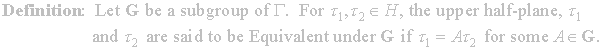
With
this we give the following definition.

We
now state a fundamental region for Γ.
![]()
We have the graphical representation of F2.
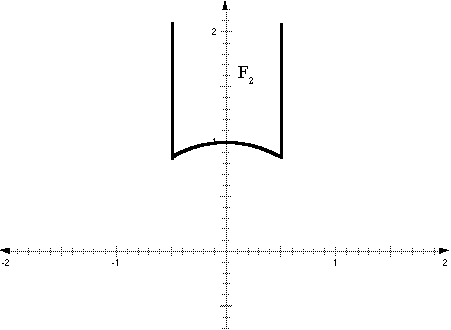
Figure 2.1
We
will prove that F2 is, in fact, a fundamental region shortly,
but first we need familiar results from lattice theory.
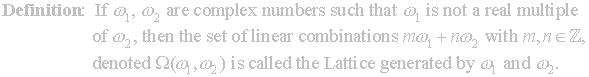


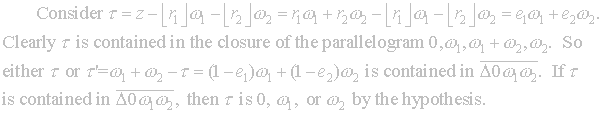

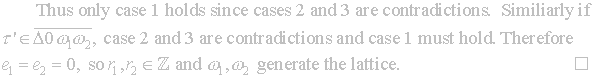
This
leads to the next theorem, for which we require the following lemma.
Theorem 2.2 is used to define the fundamental region F2.
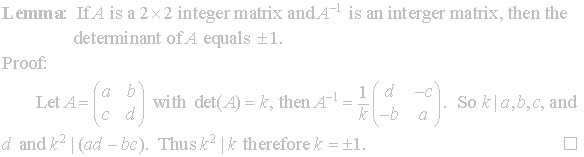
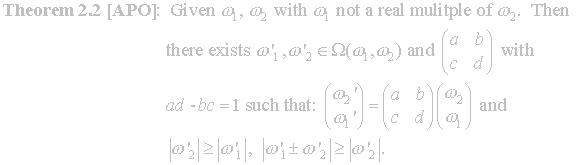
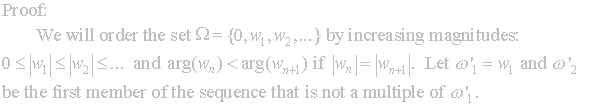

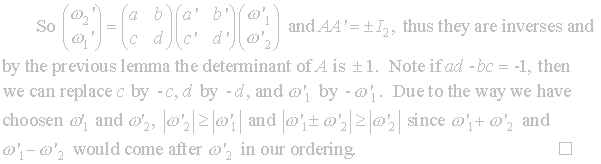
With these lattice results developed we can equate them to our points in
the upper half-plane. Theorem 2.2
gives us the existence of a matrix to map given points into a region.
Next we consider those points of the upper half-plane and the points of
the image of the mapping.

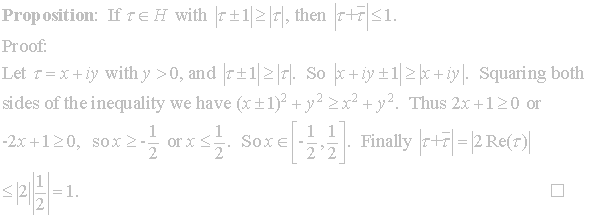
Once
we have explored the following lemma we will be ready to show that F2
(2.1) is a fundamental region for Γ.
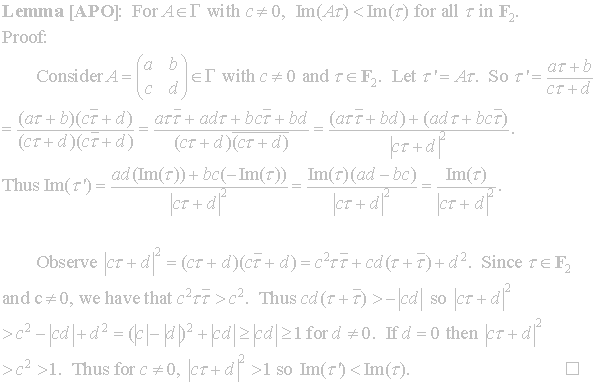
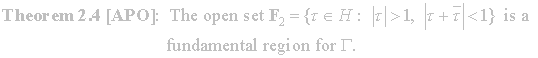
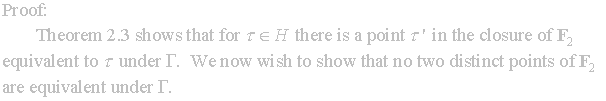
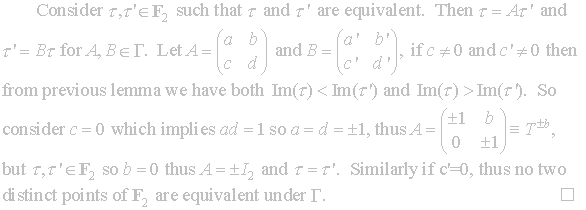
Thus
we established that F2 is a fundamental region for Γ.
Another common form of this fundamental region with defined boundaries
can be viewed with coordinates x = x and v = 1/y.
We shall see more on this form in the
![]() case.
Before we proceed with an algorithm to map points into this region, we
will take a moment to explore why we study the fundamental region.
case.
Before we proceed with an algorithm to map points into this region, we
will take a moment to explore why we study the fundamental region.

We
now explore each condition more closely. Condition
(a) states that f is analytic everywhere in H except possibly
poles, so our function acts nicely on the upper half-plane. Condition (b) states that f is invariant under all
transformations of Γ. Thus we
can see the correlation between our fundamental region and the modular function.
Property (c) is a condition on the behavior of f at the point
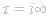 .
If
.
If
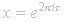 the
Fourier series in (c) is a Laurent expansion in powers of x. The behavior of f at
the
Fourier series in (c) is a Laurent expansion in powers of x. The behavior of f at
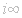 is
described by the nature of this Laurent expansion near zero.
If
is
described by the nature of this Laurent expansion near zero.
If
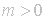 and
and
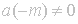 we
say that f has a pole of order m at
we
say that f has a pole of order m at
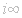 . If
. If  we say f is analytic at
we say f is analytic at
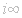 . Condition (c) states that f
has at worst a pole of order m at
. Condition (c) states that f
has at worst a pole of order m at
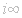 .
.