|
|
|
3. Highest-Point Algorithm for F2:
We
have shown that for any z in the upper half-plane, there exists a matrix A
in G
such that Az is in F2.
However, we have not shown how to find such an A for any given z.
For that we will employ a “highest-point” algorithm by multiplying
the matrix identified with point z by a series of Ts’ and Ss’.
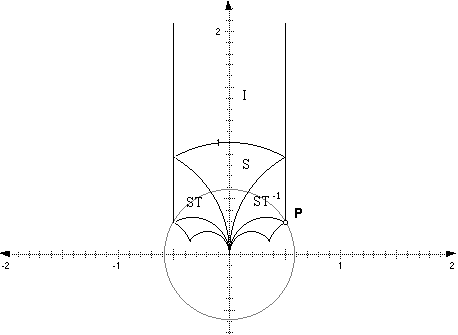
In Figure 3.1 we see how the Ts’ and Ss’ act on F2.
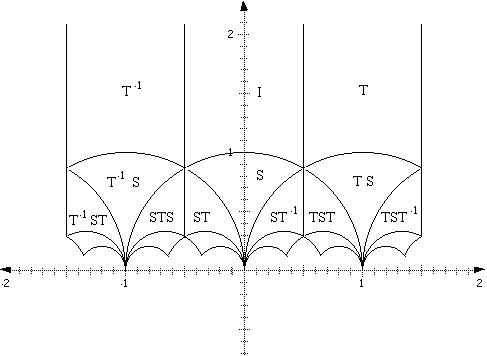
Figure
3.1
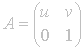 we have
we have
![]() ,
where
,
where 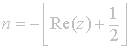 , on the left of the matrix A identified with point z.
This will move the point into the Fundamental Strip which is all points z
such that
, on the left of the matrix A identified with point z.
This will move the point into the Fundamental Strip which is all points z
such that
![]() .
.
Next
we check the norm of point
![]() , identified with matrix
, identified with matrix
![]() , to see if it is in the fundamental region.
If
, to see if it is in the fundamental region.
If
![]() then
then
![]() is in F2
and we may stop.
Else, multiply on the left of
is in F2
and we may stop.
Else, multiply on the left of
![]() by S.
We will prove shortly that this increases the imaginary part of the
associated point.
After applying the S we repeat the process until we obtain a point
in the fundamental region.
We will now formally state the algorithm.
by S.
We will prove shortly that this increases the imaginary part of the
associated point.
After applying the S we repeat the process until we obtain a point
in the fundamental region.
We will now formally state the algorithm.
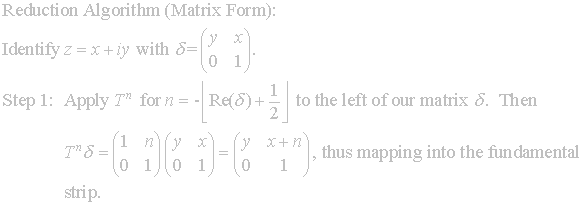
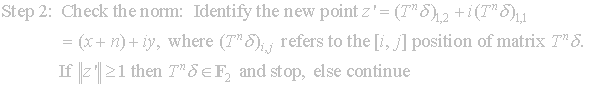
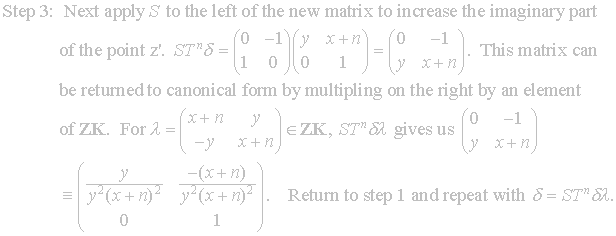
Provided the algorithm terminates we will have
![]() . Thus we can take
. Thus we can take
![]() . In order to show that this
algorithm in fact terminates, we will first prove the following theorem.
Theorem 3.1 shows the action of S on the imaginary part of z for
z not contained in the fundamental region.
. In order to show that this
algorithm in fact terminates, we will first prove the following theorem.
Theorem 3.1 shows the action of S on the imaginary part of z for
z not contained in the fundamental region.
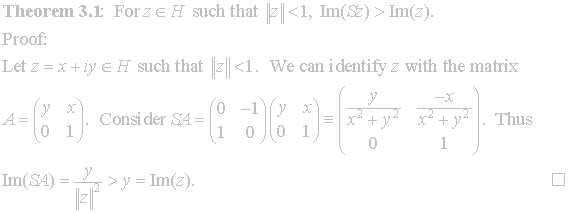

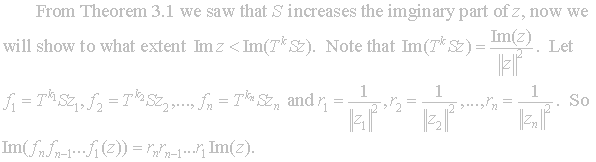

Figure
3.2
Now
we will present an example of this algorithm.
We will utilize the matrix form for our example since the point form is
similar. Refer to the appendix [A1]
for a Maple program that performs the Highest-Point Algorithm in point
form.

We
will take a brief look at the point form of the Highest-Point Algorithm for the
purpose of making an interesting note.

We
now observe the algorithm gives a particular continued fractions representation
of any point in the upper half-plane. Thus,
for z any point in the upper half-plane, there are integers
![]() such that
such that
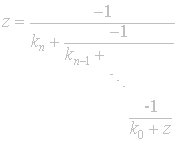 .
.
Consider the example from the matrix form of the algorithm.
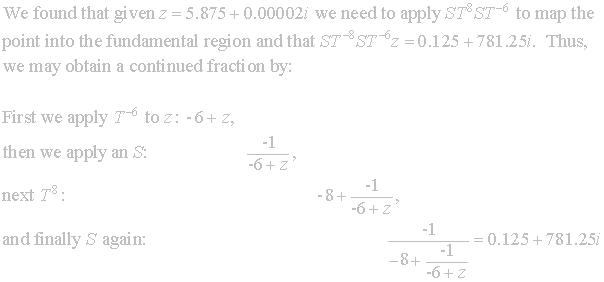
Thus we can see how applying Ts’ and Ss’ can produce a continued fraction representation.