|
|
5. Reduction Algorithm for F3
As
with the 2-dimensional case, there is an algorithm for the SP3 to
find the matrices needed to apply to a given matrix Y to map into the
fundamental region for
. Grenier’s algorithm [GGT]
is reduction algorithm since we minimize our y-coordinates.
Concurrently we are maximizing the height of Y given by 1/v
where v is the [1,1] entry of Y.
Here we also define
for matrix A.
The algorithm uses the generators Ts’, Ss’, and Us’
as in the
case.
Thus
we can see in Step 2 how the 2-dimensional case is imbedded in the
3-dimensional. A proof that
algorithm terminates and maps a given matrix into Grenier’s fundamental region
can be found in Gordon, Grenier, and Terras [GGT].
As before we will go through an example with the algorithm to gain a
better understanding, there is also a Maple program in the appendix [A2].
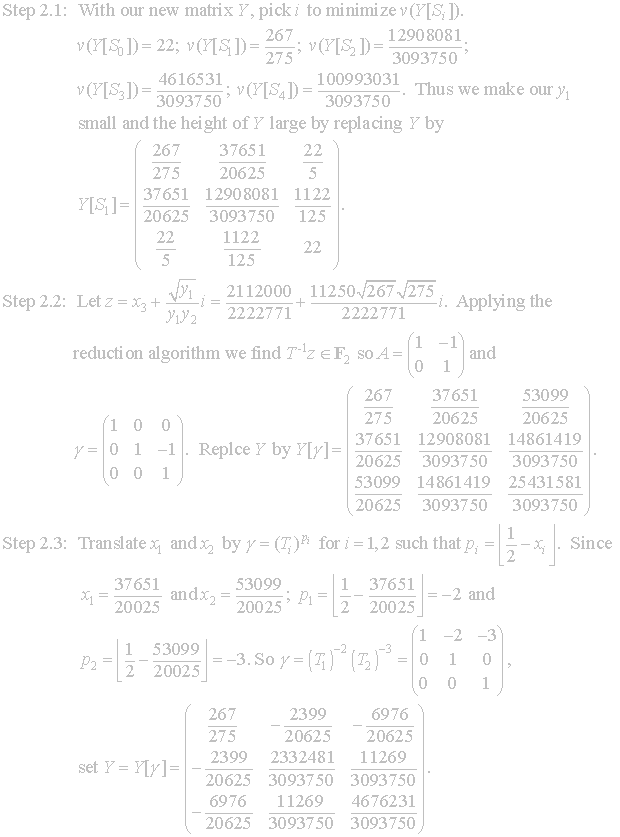
We
will stop our example at this point since the fourth iteration does not change
the matrix Y from above.
While we could check the inequalities from the fundamental region at the
end of each iteration, it clearly uses fewer resources to wait for a repeat of
the final Y.
Since our Y does not change during the next iteration we have that our
final Y given above with final coordinates:
For
this example we will check the inequalities to determine that we are, in fact,
in F3.
So as we come to the end of the paper we recall all that we have accomplished.
We developed a fundamental region for
by means of Möbius transformations
and have thoroughly examined the algorithm to move points of the upper
half-plane into the region. We have
explored the reasoning behind studying the fundamental region and have seen a
fundamental region for
. The algorithm to map points of
the upper half-space was investigated and a step-by-step example was presented.
Ultimately we can expand our knowledge as well as the canonical forms and
algorithms to higher dimensions.
And I would like to add a special thank you to Dr. Tim Flood for all the work
he
did with me to complete this project.