|
|
|
An Exotic Complex Plane
Welcome math fans to another installment of Mathematics and you.
Today we will be exploring a complex plane with an alternative
multiplication defined on it. We shall show that the plane is an algebra with this new
multiplication and standard addition. We
will also develop the Cauchy-Riemann equations and examine how common functions
act upon the plane. We begin with
our new multiplication,
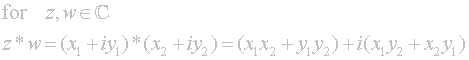
We
will denote the set of complex numbers equipped with these operations as H.
Since H has standard complex addition, all the properties for the
addition operation hold. It is
easily to verify most of the properties of the new multiplication such as
associatively, distributive, and an identity.
Scalar Multiplication also holds: r (z * w) = (r z) * w = z * (r w).
As an added bonus we also have communitivity: z * w = w * z.
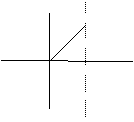
Next we develop the set of zero divisors.
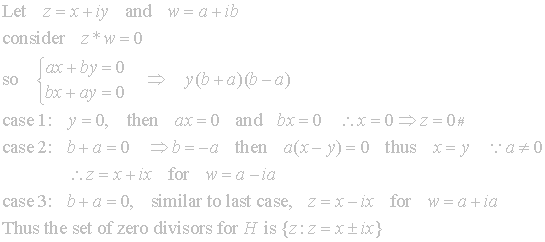
Graphically they are represented as:

With
the new definition of multiplication comes a new form of division:
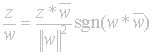 which we will use later in the
paper.
which we will use later in the
paper.
In the division defined above we have the norm, next we describe the norm
and its properties. We define the
norm of z to be ![]() .
.
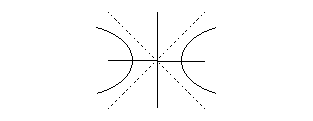
Consider the unit circle in standard complex plane, how would it be
transformed on this new plane?
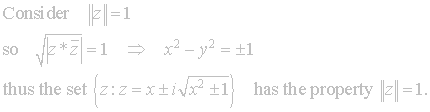
Clearly this means the union of the two
unit hyperbolas, thus our unit circle for this plane is represented as:
We can also redevelop the zero divisors of the plane using the norm,
![]()
Now we list some properties of the norm that are left to the reader to verify.
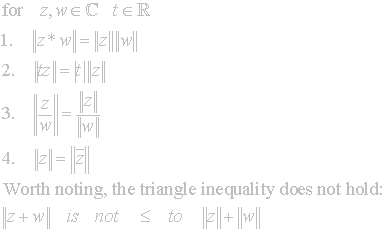
Next
let us take a more analytic look at the plane.
Will the Cauchy-Riemann equations hold for functions differentiable on
the plane? First
we define what it means to be differentiable.

If
the limit exists then f is differentiable at z0 = (x0
,y0 ) so the Cauchy-Riemann equations should exist in some form.
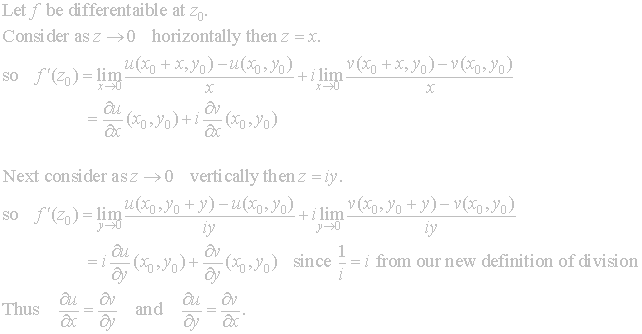
Thus
the Cauchy-Riemann equations hold in an alternate form for our plane.
As promised above we will examine how common functions act upon the
plane. With
the first example, we begin by noting that the magnitude is squared and the
‘angle’ is doubled.
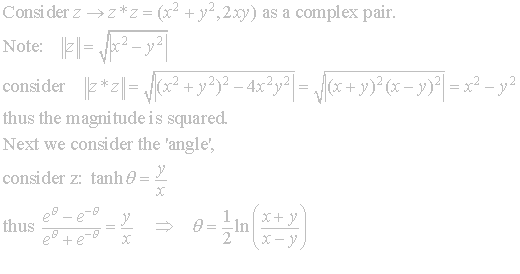

Another interesting mapping on the plane is explored below. Here we see that the mapping takes z to its scaled conjugate.

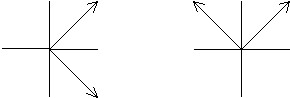
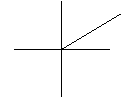
Next we will define two functions according to the hyperbolic complex plane and compare them to their natural counterparts.

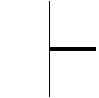
We will look at one more example of a function on our plane. Of particular interest is how the redefinition transforms an unbounded function into a bounded one.

Thus we come to the end of our look at an exotic complex plane, the
hyperbolic complex plane as we have discovered.
Along the way we have verified the algebraic properties, developed the
Cauchy-Riemann equations, and examined how some common functions act upon it.
I hope you have enjoyed this edition of Mathematics and You, thank
you and goodnight.