|
|
DI Proof
Our goal here is to develop a relationship between the number 'k' and the process f(k).
k - original number;
n - power;
d - number of digits in k;
f(k) - process of raising to power and summing the digits.
We note
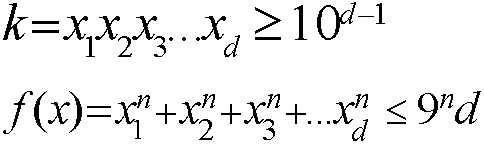
and for d > 2
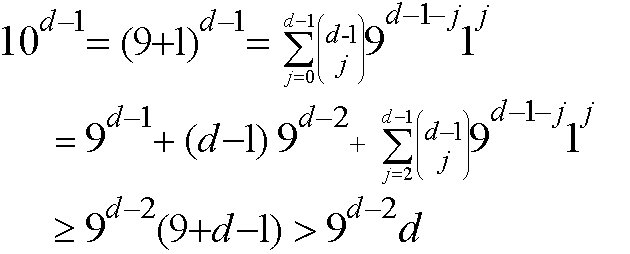
Thus, for d > n + 2, 9n d < 10d-1
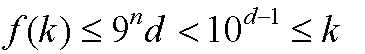
So
f(k) < k for k having n + 2 or more digits.
Theorem to be proven: Given n and k there is an m so that
f m(k) is one of the loop points.
Assume: True for all j < k and k having
n + 2 digits. So f(k) < k , and by the induction hypothesis
$ m so that f m(f(k)) is a loop point.
Therefore: once the number reaches n + 2 digits or more, f(k) becomes smaller than k.
It is not necessary to check all of the numbers below the n + 2 ceiling. If k has fewer than n + 2 then
f(k) < (n + 1)9n.
Clearly there is an a such that
(n +1)9n < a ´ 10 n.
In particular, a =4 is sufficient. This can be shown by
dividing by 9n, subtracting the left side from the right and
showing the value is positive for all n. Thus we have
h(n) = 4(10/9)n - n - 1. Differentiating this, we
h'(n) = 4(10/9)n ln(10/9) - 1 obtain , which yields a single
critical point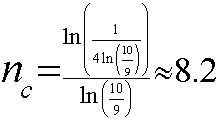 
and h(nc) » 0.29 Thus,
h(n) > 0 for all n.
Therefore, the proof will be complete if the values up to 4 ´ 10n are checked.
This provides for a healthily amount of computer time
savings. If we look at the squares: originally we had a
ceiling of d > n + 2 => testing to 999
With the new limit: 4 ´ 10n => 400 or 399 since 400 => 4
in the process.
Another computer time savings which Dr. Flood came up with was the use of nested Do loops. The idea that we were testing numbers many times was the key. When it came time to test a number, say 321, we had already tested it when we tested 123. Thus by the use of nested Do loops, we were able to cut our time dramatically. Running the eighth power on the university mainframe took 33 hours with the initial computer program.... the new version took all of 1 minute.
Please Email me with any questions or suggestions about this research. All comments are welcome.
Back to Home Page & Email